Kdjykuj

Polusa koordinatsistemo kun kelkaj anguloj indikitaj en gradoj

En matematiko, la polusa koordinata sistemo estas 2-dimensia koordinatsistemo en kiu ĉiu punkto sur ebeno estas difinita per angulo kaj distanco. La polusa koordinata sistemo estas aparte utila en situacioj, kiam la interrilato inter du punktoj estas plej facile esprimebla en terminoj de angulo kaj distanco; en la pli konata kartezia aŭ rektangula koordinatsistemo, tia angula interrilato povas esti kalkulita nur per trigonometriaj formuloj.

Ĉar la koordinatsistemo estas du-dimensia, ĉiu punkto estas difinita per du polusaj koordinatoj: la radiusa koordinato kaj la angula koordinato. La radiusa koordinato (kutime skribita kiel r{displaystyle r}) estas la distanco inter la koordinatigita punkto kaj la centra punkto de la koordinatosistemo. La centra punkto estas ankaŭ nomata poluso (ekvivalento de la origino en la Kartezia sistemo). La angula koordinato (ankaŭ nomata polusa angulo aŭ azimuta angulo, kutime skribita kiel θ aŭ t{displaystyle t}) estas la pozitiva angulo (aŭ angulo mezurita maldekstrume, malhorloĝdirekte) de la polusa akso (la 0°-a radio) al la koordinatigita punkto. La polusa akso estas ekvivalento de pozitiva duono de abscisa akso (x-akso) en la Kartezia koordinata ebeno.^[1]

Historio |

La konceptoj angulo kaj radiuso estis jam uzitaj de antikvaj matematikistoj de la 1-a jarmilo a.K.. La helena astronomo Hipparchus (-190...-120) kreis baremon de ĥordaj funkcioj donantaj la longecon de la ĥordo por ĉiu angulo, kaj ekzistas referencoj al lia uzado de polusaj koordinatoj por priskribi stelajn poziciojn.^[2]
En Pri Spiraloj, Arkimedo priskribas la Arĥimedan spiralon per funkcio kiu donas dependon de radiuso de la angulo. La greka verko, tamen, ne priskribas plenan koordinatan sistemon.

Estas diversaj historioj de la enkonduko de polusaj koordinatoj kiel parto de formala koordinatsistemo. La plena historio pri la temo estas priskribita en Fonto de Polusaj Koordinatoj fare de profesoro Julian Lowell Coolidge de Harvard^[3]Grégoire de Sanktulo-Vincent kaj Bonaventura Cavalieri sendepende prezentis la konceptojn en la mez-dek-sepa jarcento.

Sankta Vincento skribis pri ili private en 1625 kaj publikigis sian verkon en 1647, dum Cavalieri publikigis la sian en 1635 kun korektita versio aperonta en 1653. Cavalieri unue uzis polusajn koordinatojn por solvi problemon rilatan al la areo en Arĥimeda spiralo. Blaise Pascal poste uzis polusajn koordinatojn por kalkuli la longon de parabolaj arkoj.

En Maniero de Fluksionoj (skribita 1671, publikigita 1736), Siro Isaac Newton ekzamenis la transformojn inter polusaj koordinatoj, kion li nomis la "Sepa Maniero; Por Spiraloj", kaj naŭ aliaj koordinatsistemoj).^[4] En la ĵurnalo Acta Eruditorum (1691), Jakobo Bernoulli uzis sistemon kun punkto sur linio, nomitaj kiel poluso kaj polusa akso respektive.
Koordinatoj estis precizigitaj per la distanco de la poluso kaj la angulo de la polusa akso. La verko de Bernoulli ampleksis trovi la kurbecoradiuson de kurboj esprimitaj per tiaj koordinatoj.

La efektiva termino polusaj koordinatoj estas atribuita al Gregorio Fontana kaj estis uzata de Italaj skribistoj de la 18-a jarcento. La termino) aperis en la angla en traduko (1816) fare de Georgo Peacock de Diferencialo kaj Integrala Kalkulo fare de Lacroix.^[5][6]Alexis Clairaut estis la unua kiu konceptis polusajn koordinatojn en tri dimensioj, kaj Leonhard Euler estis la unua kiu reale ellaboris ilin.^[3]

Grafika prezentado de punktoj per polusaj koordinatoj |

La punktoj (3,60°) kaj (4,210°) per polusa koordinata sistemo

Ĉiu punkto en la polusa koordinata sistemo povas esti priskribita per la du polusaj koordinatoj, kiuj estas kutime signitaj r{displaystyle r} (la radiusa koordinato) kaj θ (la angula koordinato, polusa angulo, aŭ azimuta angulo, fojfoje prezentita kiel φ aŭ t{displaystyle t}). La koordinato r{displaystyle r} prezentas la radiusan distancon de la poluso, kaj la koordinato θ prezentas la mallaŭ-horloĝnadla (kontraŭhorloĝnadla) angulo de la radio 0° (iam nomata la polusa akso), konata kiel la pozitiva abscisa akso sur la Kartezia koordinata ebeno.^[1]

Ekzemple, la polusaj koordinatoj (3, 60°) estus grafike prezentitaj kiel punkto 3 unuojn disde la poluso sur la radio 60°.
La koordinatoj (−3, 240°) ankaŭ estus grafike prezentitaj ĉe ĉi tiu punkto ĉar negativa radiusa distanco estas montrita kiel pozitiva distanco sur la kontraŭa radio (la radio reflektita ĉirkaŭ la fonto, kiu diferencas de la originala radio je 180°).

Ĉi tio ilustras unu gravan aspekton de la polusa koordinata sistemo ne ĉeesta en la Kartezia koordinatsistemo: sola punkto povas esti esprimita per malfinia nombro de malsamaj koordinatoj. En generalo, la punkto (r{displaystyle r}, θ) povas esti prezentita kiel (r{displaystyle r}, θ ± n{displaystyle n}×360°) aŭ (−r{displaystyle r}, θ ± (2n{displaystyle n} + 1)×180°), kie n{displaystyle n} estas iu ajn entjero.^[7] La ajnecaj koordinatoj (0, θ) estas konvencie uzataj por prezenti la poluson, ĉar sendistinge de la koordinato θ, punkto kun radiuso 0 estos ĉiam esti sur la poluso.^[8] Por akiri unikan prezenton de punkto, estas kutime limigi r{displaystyle r} al nenegativaj nombroj, r{displaystyle r} ≥ 0 kaj θ al la intervalo [0, 360°) aŭ (−180°, 180°] (aŭ, en radiana mezurado, [0, 2π) aŭ (−π, π]).^[9]

Anguloj en polusa notacio estas ĝenerale esprimitaj en aŭ gradoj aŭ radianoj, uzante la konvertiĝon 2π rad = 360°. La elekto dependas grande de la ĉirkaŭteksto. Navigadaj aplikoj uzas grado-mezuradon, dum iuj fizikaj aplikoj (aparte turna mekaniko) kaj preskaŭ ĉiu matematika literaturo sur kalkulo uzas radiano-mezurado.^[10]

Konvertado inter polusaj kaj karteziaj koordinatoj |

Figuro ilustranta la formulojn de konvertado

La du polusaj koordinatoj r{displaystyle r} kaj θ povas esti konvertitaj al la karteziaj koordinatoj x{displaystyle x} kaj y{displaystyle y} per uzo de la trigonometriaj funkcioj sinuso kaj kosinuso:

x=rcos⁡θ{displaystyle x=rcos theta ,}

y=rsin⁡θ,{displaystyle y=rsin theta ,,}

kaj la du karteziaj koordinatoj x{displaystyle x} kaj y{displaystyle y} povas esti konvertitaj al polusa koordinato r{displaystyle r} per

r=x2+y2{displaystyle r={sqrt {x^{2}+y^{2}}},} (per simpla apliko de la Pitagora teoremo).

Por kalkuli la angulan koordinaton θ, la konsiderendas ke:

• Por r{displaystyle r} = 0, θ povas esti iu ajn reela nombro.


• Por r{displaystyle r} ≠ 0, por ricevi unikan prezenton pri θ, necesas limigi intervalon kie ĝi povas esti al amplekso de 2π. Kutimaj elektoj por tia intervalo estas [0, 2π) kaj (−π, π].

Por ricevi θ en la intervalo [0, 2π), la jena formulo uzeblas: (arctan{displaystyle arctan } estas la inverso de tangenta funkcio):

θ={arctan⁡(yx)se x>0 kaj y≥0arctan⁡(yx)+2πse x>0 kaj y<0arctan⁡(yx)+πse x<0π2se x=0 kaj y>03π2se x=0 kaj y<0{displaystyle theta ={begin{cases}arctan({frac {y}{x}})&{mbox{se }}x>0{mbox{ kaj }}ygeq 0\arctan({frac {y}{x}})+2pi &{mbox{se }}x>0{mbox{ kaj }}y<0\arctan({frac {y}{x}})+pi &{mbox{se }}x<0\{frac {pi }{2}}&{mbox{se }}x=0{mbox{ kaj }}y>0\{frac {3pi }{2}}&{mbox{se }}x=0{mbox{ kaj }}y<0end{cases}}}

Por ricevi θ en la intervalo (−π, π], la jena formulo uzeblas:

θ={arctan⁡(yx)se x>0arctan⁡(yx)+πse x<0 kaj y≥0arctan⁡(yx)−πse x<0 kaj y<0π2se x=0 kaj y>0−π2se x=0 kaj y<0{displaystyle theta ={begin{cases}arctan({frac {y}{x}})&{mbox{se }}x>0\arctan({frac {y}{x}})+pi &{mbox{se }}x<0{mbox{ kaj }}ygeq 0\arctan({frac {y}{x}})-pi &{mbox{se }}x<0{mbox{ kaj }}y<0\{frac {pi }{2}}&{mbox{se }}x=0{mbox{ kaj }}y>0\-{frac {pi }{2}}&{mbox{se }}x=0{mbox{ kaj }}y<0end{cases}}}

(En diversaj programadlingvoj oni povas teni distingaj la numeratoron kaj la denominatoron per uzo de la funkcio atan2, kiu havas apartajn argumentojn por tiuj du.)

Polusaj ekvacioj |

La ekvacia difino de algebra kurbo esprimita en polusaj koordinatoj estas nomata polusa ekvacio. En multaj okazoj tia ekvacio povas esti donita per difinado de r{displaystyle r} kiel funkcio de θ. La rezultanta kurbo tiam konsistas el punktoj de formo (r{displaystyle r}(θ), θ) kaj konsidereblas la grafikaĵo de la polusa funkcio r{displaystyle r}.

Malsamaj formoj de simetrio povas esti konkluditaj de la ekvacio de polusa funkcio r{displaystyle r}. Se r{displaystyle r}(−θ) = r{displaystyle r}(θ), la kurbo estas simetria ĉirkaŭ la horizontala (0°/180°) akso (absciso); se r{displaystyle r}(π−θ) = r{displaystyle r}(θ), ĝi estas simetria ĉirkaŭ la vertikala (90°/270°) akso (ordinato), kaj se r{displaystyle r}(θ−α°) = r{displaystyle r}(θ), ĝi estas turne simetria je α° (laŭhorloĝnadle kaj samtempe kontraŭhorloĝnadle) ĉirkaŭ la poluso.

Pro la cirkla naturo de la polusa koordinata sistemo, multaj kurboj povas esti priskribitaj per iom pli simplaj polusaj ekvacioj, ol siaj ekvacioj en karteziaj koordinatoj. Inter la plej bone konata de tiaj kurboj estas la polusa rozo, Arĥimeda spiralo, lemniskato, heliko de Pascal, kaj kardioido. ,

Cirklo |

Cirklo kun ekvacio r{displaystyle r}(θ) = 1

La ĝenerala ekvacio por cirklo kun centro je (r{displaystyle r}₀, φ) kaj radiuso a{displaystyle a} estas

r2−2rr0cos⁡(θ−φ)+r02=a2.{displaystyle r^{2}-2rr_{0}cos(theta -varphi )+r_{0}^{2}=a^{2}.,}

Ĝi povas esti plisimpligita diversmaniere, por specifaj kazoj. Por cirklo kun centro je la poluso kaj radiuso a{displaystyle a} la ekvacio estas

r(θ)=a{displaystyle r(theta )=a,} .^[11]

Linio |

Radiusaj duonlinioj (tiuj komenciĝas en la poluso) estas prezentataj per ekvacio

θ=φ{displaystyle theta =varphi },

kie φ estas la angulo de alteco de la duonlinio;

Radiusaj linioj (tiuj kiuj iras tra la poluso) estas prezentataj per ekvacio

θ=φ{displaystyle theta =varphi } aŭ θ=φ+π{displaystyle theta =varphi +pi },

kie φ estas la angulo de alteco de la linio; φ = arctan⁡(m){displaystyle arctan(m)} kie m{displaystyle m} estas la angula koeficiento de la linio en la karteziaj koordinatoj. En ĉi tiu ekvacio unu duono (θ=φ{displaystyle theta =varphi }) respektivas al unu duonlinio kaj la alia (θ=φ+π{displaystyle theta =varphi +pi }) respektivas al duonlinio en la mala direkto; kune ili formas rektan linion.

La ne-radiusa linio, kiu krucas la radiusan linion θ = φ perpendikulare en punkto (r{displaystyle r}₀, φ) havas la ekvacion

r(θ)=r0sec⁡(θ−φ){displaystyle r(theta )={r_{0}}sec(theta -varphi )}.

Polusa rozo |

Polusa rozo per ekvacio
r{displaystyle r}(θ) = 2 sin (4θ)

Polusa rozo estas fama matematika kurbo, kiu aspektas simile al floro, kaj kiu povas esti esprimita per simpla polusa ekvacio. Ĝi estas donita per ekvacioj

r(θ)=acos⁡(kθ+ϕ0){displaystyle r(theta )=acos(ktheta +phi _{0})},

aŭ

r(θ)=asin⁡(kθ+ϕ0){displaystyle r(theta )=asin(ktheta +phi _{0})}, por ia ajn konstanto ϕ0{displaystyle phi _{0}} (inkluzive de 0).

Se k estas entjero, tiuj ekvacioj produktas k-folian rozon se k estas nepara, aŭ 2k-folian rozon se k estas para. Se k estas racionalo neentjera, rozeska formo povas formiĝi sed kun intersurkuŝantaj folioj.
Se k estas neracionala, la kurbo konsistigas densan aron en la disko r<=a. Notu, ke ĉi tiuj ekvacioj neniam difinas rozon kun 2, 6, 10, 14, kaj tiel plu folioj. La variablo a prezentas la longecon de la folioj de la rozo.

Arĥimeda spiralo |

Unudirekta Arĥimeda spiralo kun ekvacio
r(θ) = θ
por 0 < θ < 6π

La Arĥimeda spiralo estas fama spiralo, kiu estis malkovrita de Arkimedo, kiu ankaŭ povas esti esprimita kiel simpla polusa ekvacio. Ĝin prezentas la ekvacio

r(θ)=a+bθ.{displaystyle r(theta )=a+btheta .,}

Ŝanĝado de la parametro a turnas la spiralon, dum b regas la distancon inter la bukloj, kiu por donita spiralo estas ĉiam konstanto. La Arĥimeda spiralo havas du branĉojn, unu por θ > 0 kaj unu por θ < 0. La du branĉoj estas glate koneksaj en la poluso. Prenado de la spegulita bildo de unu branĉo trans la linio 90°/270° liveras la alia branĉon. Ĉi tiu kurbo estas rimarkinda kiel unu el la unuaj kurboj, post la konikoj, priskribitaj en matematika traktato, kaj kiel elstara ekzemplo de kurbo kiun plej bone difinas polusa ekvacio.

Konikoj |

Elipso, montranta duonan latusan rektumon (vidu tekston)

La ekvacio de koniko kun unu fokuso sur la poluso kaj la alia ie sur la radio 0° (tiel ke la granda akso de la koniko kuŝas laŭ la polusa akso) estas donita per:

r(θ)=ℓ1+ecos⁡θ{displaystyle r(theta )={ell over {1+ecos theta }}}

kie e estas la (discentreco, fokusdiseco) kaj ℓ{displaystyle ell } estas la duone-latus rektumo (la perpendikulara distanco je fokuso de la granda akso al la kurbo). Se e > 1, ĉi tiu ekvacio difinas hiperbolo (matematiko)n; se e = 1, ĝi difinas parabolo (matematiko)n; kaj se e < 1, ĝi difinas elipson.
La speciala kazo e = 0 de tiu lasta liveras cirklon de radiuso ℓ{displaystyle ell }.

Kompleksaj nombroj |

Bildo de kompleksa nombro z grafike prezentita sur la kompleksa ebeno

Ĉiu kompleksa nombro povas esti prezentita kiel punkto en la kompleksa ebeno, kaj povas pro tio esti esprimita aŭ per siaj karteziaj koordinatoj (la prezento estas nomata ankaŭ rektangula aŭ kartezia formo), aŭ per la polusaj koordinatoj de la punkto (la polusa varianto estas nomata ankaŭ trigonometria prezento, aŭ polusa formo). La kompleksa nombro z prezenteblas kartezie per

z=x+iy{displaystyle z=x+iy,}

kie i estas la imaginara unuo, povas alternative esti skribita en trigonometria prezento (per la konvertaj formuloj donitaj pli supre) per

z=r⋅(cos⁡θ+isin⁡θ){displaystyle z=rcdot (cos theta +isin theta )}

kaj de tio per

z=reiθ{displaystyle z=re^{itheta },}

kie e estas la bazo de naturaj logaritmoj, kiuj estas ekvivalentaj kiel montrite per la eŭlera formulo.^[12] (Notu ke tiu formulo, simile al ĉiuj tiuj engaĝantaj eksponentojn de anguloj, bezonas ke la angulo θ estu esprimita en radianoj.)

Por la operacioj multipliko, divido, kaj potencigo de kompleksaj nombroj, estas ĝenerale pli simple labori kun kompleksaj nombroj esprimitaj en trigonometria formo en ol rektangula formo. De la leĝoj de potencigo sekvas ke:

• Multipliko:

r0eiθ0⋅r1eiθ1=r0r1ei(θ0+θ1){displaystyle r_{0}e^{itheta _{0}}cdot r_{1}e^{itheta _{1}}=r_{0}r_{1}e^{i(theta _{0}+theta _{1})},}

• Divido:

r0eiθ0r1eiθ1=r0r1ei(θ0−θ1){displaystyle {frac {r_{0}e^{itheta _{0}}}{r_{1}e^{itheta _{1}}}}={frac {r_{0}}{r_{1}}}e^{i(theta _{0}-theta _{1})},}

• Potencigo (de formulo de de Moivre):

(reiθ)n=rneinθ{displaystyle (re^{itheta })^{n}=r^{n}e^{intheta },}

Kalkulo |

Kalkulo povas esti aplikita al ekvacioj esprimitaj en polusaj koordinatoj.^[13][14]

La angula koordinato θ estas esprimita en radianoj ĉie en ĉi tiu sekcio, kio estas la kutima elekto en kalkulo.

Diferenciala kalkulo |

Ni havas jenajn formulojn:

r∂∂r=x∂∂x+y∂∂y{displaystyle r{tfrac {partial }{partial r}}=x{tfrac {partial }{partial x}}+y{tfrac {partial }{partial y}},}

∂∂θ=−y∂∂x+x∂∂y.{displaystyle {tfrac {partial }{partial theta }}=-y{tfrac {partial }{partial x}}+x{tfrac {partial }{partial y}}.}

Por trovi la kartezian angulan koeficienton de la tanĝa linio al polusa kurbo r(θ) je iu ajn donita punkto, la kurbo estu unue esprimita kiel sistemo de parametraj ekvacioj.

x=r(θ)cos⁡θ{displaystyle x=r(theta )cos theta ,}

y=r(θ)sin⁡θ{displaystyle y=r(theta )sin theta ,}

Derivi ambaŭ ekvaciojn kun respekto al θ liveras

∂x∂θ=r′(θ)cos⁡θ−r(θ)sin⁡θ{displaystyle {tfrac {partial x}{partial theta }}=r'(theta )cos theta -r(theta )sin theta ,}

∂y∂θ=r′(θ)sin⁡θ+r(θ)cos⁡θ{displaystyle {tfrac {partial y}{partial theta }}=r'(theta )sin theta +r(theta )cos theta ,}

Dividado de la dua ekvacio per la unua liveras la kartezian angulan koeficienton de la tanĝa linio al la kurbo je la punkto (r, θ):

dydx=r′(θ)sin⁡θ+r(θ)cos⁡θr′(θ)cos⁡θ−r(θ)sin⁡θ{displaystyle {frac {dy}{dx}}={frac {r'(theta )sin theta +r(theta )cos theta }{r'(theta )cos theta -r(theta )sin theta }}}

Integrala kalkulo |

La integralada regiono R estas barita per la kurbo r(θ) kaj la radioj θ = a kaj θ = b.

Lasu ke R signu la regionon enlimigitan per kurbo r(θ) kaj la radioj θ = a kaj θ = b, kie 0 < b − a < 2π. Tiam, la areo de R estas

12∫abr(θ)2dθ.{displaystyle {frac {1}{2}}int _{a}^{b}r(theta )^{2},dtheta .}

La regiono R estas aproksimita per n sektoroj (ĉi tie, n = 5).

Tiu rezulto troveblas jenamaniere. Unue, la intervalo [a, b] estas dividita en n subintervalojn, kie n estas ajneca pozitiva entjero.
Tial Δθ, la longo de ĉiu subintervalo, estas egala al b − a (la tuta longo de la intervalo), dividita per n, la nombro de subintervaloj. Por ĉiu subintervalo i = 1, 2, …, n, lasu ke θ_i estu la mezpunkto de la subintervalo, kaj konstruu sektoron kun la centro je la poluso, radiuso r(θ_i), kaj centra angulo Δθ. La areo de ĉiu konstruita sektoro estas pro tio egala al 12r(θi)2Δθ{displaystyle {tfrac {1}{2}}r(theta _{i})^{2}Delta theta }. De tio, la tuta areo de ĉiuj sektoroj estas

∑i=1n12r(θi)2Δθ.{displaystyle sum _{i=1}^{n}{tfrac {1}{2}}r(theta _{i})^{2},Delta theta .}

Dum la nombro de subintervaloj n estas multigita, la proksimuma kalkulado de la areo daŭras pliboniĝi. En la limigo kiel n → ∞, la sumo iĝas la Rimana sumo por la integralo supre.

Ĝeneraligo |

Per uzo de Karteziaj koordinatoj, infinitezima area ero povas esti kalkulita kiel da = dx dy. La regulo por integralado per anstataŭigo de variabloj en oblaj integraloj diras, ke, kiam oni uzas aliajn koordinatojn, la jakobia determinanto (jakobiano J) de la koordinata konvertiĝa formulo devas esti konsiderata:

J=det∂(x,y)∂(r,θ)=|∂x∂r∂x∂θ∂y∂r∂y∂θ|=|cos⁡θ−rsin⁡θsin⁡θrcos⁡θ|=rcos2⁡θ+rsin2⁡θ=r.{displaystyle J=det {frac {partial (x,y)}{partial (r,theta )}}={begin{vmatrix}{frac {partial x}{partial r}}&{frac {partial x}{partial theta }}\{frac {partial y}{partial r}}&{frac {partial y}{partial theta }}end{vmatrix}}={begin{vmatrix}cos theta &-rsin theta \sin theta &rcos theta end{vmatrix}}=rcos ^{2}theta +rsin ^{2}theta =r.}

Do, area ero en polusaj koordinatoj povas esti skribita kiel

dA=|J|drdθ=rdrdθ.{displaystyle dA=|J|,dr,dtheta =r,dr,dtheta .}

Nun, funkcio donita en polusaj koordinatoj povas esti integralita kiel sekvas:

∬Rf(r,θ)dA=∫ab∫0r(θ)f(r,θ)rdrdθ.{displaystyle iint _{R}f(r,theta ),dA=int _{a}^{b}int _{0}^{r(theta )}f(r,theta ),r,dr,dtheta .}

Ĉi tie, R estas la sama regiono kiel pli supre, nome, la regiono enlimigita per kurbo r(θ) kaj la radioj θ = a kaj θ = b.

La formulo por la areo de R menciita pli supre estas trovita per tio preni f idente egala al 1. Pli surpriza apliko de tiu rezulto liveras la Gaŭsan intergralon

∫−∞∞e−x2dx=π.{displaystyle int _{-infty }^{infty }e^{-x^{2}},dx={sqrt {pi }}.}

Vektora kalkulo |

Vektora kalkulo povas ankaŭ esti aplikata al polusaj koordinatoj. Lasu ke r{displaystyle mathbf {r} } estu la radiusvektoro (rcos⁡(θ),rsin⁡(θ)){displaystyle (rcos(theta ),rsin(theta )),}, kun r kaj θ{displaystyle theta } dependantaj de tempo t, r^{displaystyle {hat {mathbf {r} }}} estu unuobla vektoro en la direkto r{displaystyle mathbf {r} } kaj θ^{displaystyle {hat {boldsymbol {theta }}}} estu unuobla vektoro ortaj al r{displaystyle mathbf {r} }. La unua kaj dua derivaĵoj de pozicio estas

drdt=r˙r^+rθ˙θ^,{displaystyle {frac {dmathbf {r} }{dt}}={dot {r}}{hat {mathbf {r} }}+r{dot {theta }}{hat {boldsymbol {theta }}},}

d2rdt2=(r¨−rθ˙2)r^+(rθ¨+2r˙θ˙)θ^.{displaystyle {frac {d^{2}mathbf {r} }{dt^{2}}}=({ddot {r}}-r{dot {theta }}^{2}){hat {mathbf {r} }}+(r{ddot {theta }}+2{dot {r}}{dot {theta }}){hat {boldsymbol {theta }}}.}

Tri dimensioj |

La polusa koordinata sistemo estas etendita en tri dimensiojn per du malsamaj koordinataj sistemoj: la cilindra kaj la sfera koordinato-sistemoj, kiuj ambaŭ inkluzivas dudimensiajn (aŭ ebenecajn) polusajn koordinatojn kiel subaro. La cilindra koordinata sistemo etendas polusajn koordinatojn per aldono de distanca koordinato, kaj la sfera sistemo anstataŭe aldonas angulan koordinaton.

Cilindraj koordinatoj |

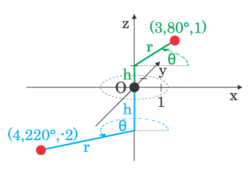
2 punktoj grafike prezentitaj per cilindraj koordinatoj

La cilindra koordinata sistemo estas koordinatsistemo kiu etendas la du-dimensian polusan koordinatan sistemon per aldono de tria koordinato, kiu estas la alto de punkto super la ebeno, simile al la maniero per kiu la karteziaj koordinatoj estas etendita en tri dimensiojn. La tria koordinato estas kutime skribata h, kaj do estas la tri cilindraj koordinatoj (r, θ, h).

La tri cilindraj koordinatoj povas esti konvertita al karteziaj koordinatoj per

x=rcos⁡θy=rsin⁡θz=h.{displaystyle {begin{aligned}x&=r,cos theta \y&=r,sin theta \z&=h.end{aligned}}}

Sferaj koordinatoj |

Punkto grafike prezentitaj uzantaj sferaj koordinatoj

Sfero kun krado de sferaj koordinatoj. ρ estas konstanto. Estas montritaj du familioj de linioj - kun φ konstanta kaj kun θ konstanta.

Polusaj koordinatoj ankaŭ povas esti etenditaj en tri dimensiojn kiel sfera koordinata sistemo de koordinatoj (ρ, φ, θ), kie ρ estas la distanco de la fonto, φ estas la angulo de la z-akso (nomata kiel la zenita distanco^[15], ĝi estas inter 0 kaj 180°) kaj θ estas la angulo de la abscisa akso (kiel en la 2-dimensiaj polusaj koordinatoj). Ĉi tiu koordinatsistemo estas simila al la latitudo kaj longitudo uzataj por geografio, kun la fonto en la centro de Tero, la latitudo δ estas la komplemento de φ, difinita kiel δ = 90° − φ, kaj la longitudo l estas l = θ , ĉi tie l estas inter −180° kaj −180°.^[16]

La tri sferaj koordinatoj estas konvertataj al karteziaj koordinatoj per

x=ρsin⁡ϕcos⁡θy=ρsin⁡ϕsin⁡θz=ρcos⁡ϕ.{displaystyle {begin{aligned}x&=rho ,sin phi ,cos theta \y&=rho ,sin phi ,sin theta \z&=rho ,cos phi .end{aligned}}}

Aplikoj |

Polusaj koordinatoj estas du-dimensiaj kaj tial ili povas esti uzataj nur kiam punkto-pozicioj kuŝas sur sola du-dimensia ebeno. Ili estas plej adekvataj en iu ajn ĉirkaŭteksto kie la fenomeno konsiderata estas imanente ligita al direkto kaj longo de centra punkto. Ekzemple, la ekzemploj supre montras kiel rudimentaj polusaj ekvacioj sufiĉas por difini kurbojn – kiaj la Arĥimeda spiralo – kies ekvacio en la Kartezia koordinato estus multe pli komplika. Ankaŭe, multaj fizikaj sistemoj – kiaj tiuj koncernitaj kun korpoj movantaj ĉirkaŭ centra punkto aŭ kun fenomenoj devenantaj de centra punkto – estas pli simplaj kaj pli intuiciaj por modeli per uzo de polusaj koordinatoj. La komenca motivado por la enkonduko de la polusa sistemo estis la studo de cirkla kaj orbita moviĝo de objekto.

Pozicio kaj navigado |

Polusaj koordinatoj estas uzataj ofte en navigado, ĉar la celo aŭ direkto de vojaĝo povas esti donita kiel angulo kaj distanco de la objekto konsiderata. Ekzemple, la aviadilo uzas iomete modifitan version de la polusaj koordinatoj por navigado. En tiu sistemo, tiu ĝenerale uzata por ia ajn navigado, la radio 0° estas ĝenerale nomata frontado 360, kaj la anguloj daŭras en laŭhorloĝnadla direkto, anstataŭ kontraŭhorloĝnadla, kiel en la matematika sistemo. Frontado 360 respondas al norda magnetpoluso, dum frontadoj 90, 180, kaj 270 respondas al magneta oriento, sudo, kaj okcidento, respektive.^[17] Tial, aviadilo vojaĝanta 5 marmejlojn precize orienten estas vojaĝanta 5 unuojn je frontado 90 (legu niner-zero (angla prononco: nAJnerzIro) laŭ aer-trafika rego).^[18]

Modelado |

Sistemoj elmontrantaj radiusan simetrion provizas naturajn mediojn por la polusa koordinata sistemo, kun la centra punkto agante kiel la poluso. Unuaranga ekzemplo de ĉi tiu uzado estas la ekvacio de terakva fluo kiam aplikita al radiuse simetriaj fluoj ĉirkaŭ putoj. Sistemoj kun radiusa forto ankaŭ estas bonaj kandidatoj por la uzo de la polusa koordinata sistemo. Tiaj sistemoj inkluzivas gravitajn kampojn, kiuj obeas la inverso-kvadratan leĝon, aldone al sistemoj kun punktaj fontoj, kiaj radiofon-antenoj.

Radiuse malsimetriaj sistemoj povas ankaŭ esti modelitaj per polusaj koordinatoj. Ekzemple, mikrofona sensilo-ŝablono ilustras ĝian proporcian respondon al envenanta sono el donita direkto, kaj ĉi tiuj ŝablonoj povas esti prezentitaj kiel polusaj kurboj. La kurbo por norma kardioida mikrofono, la plej komuna unudirekta mikrofono, povas esti prezentita kiel r = 0.5 + 0.5 sin θ.^[19]

Referencoj |

Ĝeneralaj

• ANTON, Howard; Irl Bivens, Stephen Davis. (2002) Calculus - Kalkulo, ‑a eldono, Anton Textbooks, Inc. - Anton Lernolibroj, Inc.. ISBN 0-471-38157-8.


• FINNEY, Ross; Georga Tomaso, Franklin Demana, Bert Atendas. (junio 1994) Calculus: Graphical, Numerical, Algebraic - Kalkulo: Grafika, Cifereca, Algebra, ‑a eldono, Addison-Wesley Publishing Co. - Addison-Wesley Publikiganta Co.. ISBN 0-201-55478-X.

Specifaj

Eksteraj ligiloj |

• FooPlot (surlinia funkcia desegnilo en polusaj koordinatoj)


• Surlinia konvertiĝa laborilo inter polusa kaj karteziaj koordinatoj

Ĉi tiu artikolo estis je 7 aprilo 2007 akceptita en la liston de elstaraj artikoloj.

Tiu ĉi artikolo estis artikolo de la semajno en la 17-a semajno de la jaro 2007.

Tiu ĉi artikolo estis artikolo de la semajno en la 18-a semajno de la jaro 2018.