Kdjykuj

La botelo de Klein mergita en tri-dimensian spacon.

En matematiko, la botelo de Klein estas certa 2-dimensia dukto, tio estas, surfaco. Ĝi estas kompakta kaj ne-orientebla (sen malsamaj ena kaj ekstera flankoj). Botelo de Klein ne povas esti enigita en kutiman tri-dimensian eŭklidan spacon sen sekco de si.

Ĝia eŭlera karakterizo estas 0.

Aliaj rilatantaj ne-orienteblaj objektoj estas la filmo de Möbius kaj la reela projekcia ebeno. Rilatantaj orienteblaj objektoj estas cilindro, sfero kaj toro. Filmo de Möbius kaj cilindro estas du dimensiaj surfacoj kun rando; botelo de Klein, reela projekcia ebeno, sfero kaj toro ne havas randon.

La botelo de Klein estis unua priskribis en 1882 per la germana matematikisto Felix Klein. Ĝi estis originale nomata kiel Kleinsche Fläche, "surfaco de Klein"; tamen, ĉi tiu estis malĝuste interpretita kiel Kleinsche Flasche, "Botelo de Klein". Finfine la lasta varianto estis adoptita ankaŭ en la germana lingvo.

Konstruado |

Startu de kvadrato kaj tiam gluu kune respektivajn kolorigitajn randoj, tiel ke la sagoj kongruu. Botelo de Klein estas la kvocienta spaco priskribis kiel unuobla kvadrato ( [0,1] × [0,1] ) kun flankoj identigitaj per la rilatoj:

(0, y) ~ (1, y) por 0 ≤ y ≤ 1

(x, 0) ~ (1-x, 1) por 0 ≤ x ≤ 1

Ĉi tiu kvadrato estas fundamenta plurlatero de la botelo de Klein.

Sfero	Cilindra surfaco	Rubando de Möbius
Toro	Botelo de Klein	Reela projekcia ebeno

Noto ke ĉi tio estas abstrakta gluado en topologia senco.

Botelo de Klein ne povas esti enigita (tio estas sen sinsekco) en tri-dimensian spacon. Tamen, ĝi povas esti mergita (lokaj najbaraĵoj ne havas sinsekcojn).

Glui la ruĝajn sagoj de la kvadrato kune, rezultiĝas cilindro. Por glui la bluajn sagojn kune, traigu unu finon tra la flanko de la cilindro. Ĉi tiu kreas cirklon de sinsekco. Ĉi tiu estas mergo de la botelo de Klein en tri dimensioj.

Botelo de Klein povas esti enigita en 4-dimensian eŭklidan spacon. Anstataŭ sinsekco, eblas ĉirkaŭ iri per la 4-a dimensio. Utila analogeco estas konsideri sinsekcantan kurbo sur la ebeno; sinsekco povas esti eliminita per movo de unu el la intersekcantaj eroj de la kurbo for de la ebeno en la 3-an dimension.

Ses koloroj sufiĉas por kolorigo de ĉiu mapo sur botelo de Klein; ĉi tio estas la nura escepto al
la konjekto de Heawood, ĝeneraligo de la teoremo de kvar koloroj, kiu devus postuli sep kolorojn.

Botelo de Klein estas ekvivalento al sfero plus du kruco-ĉapoj.

Botelo de Klein (imitado)

La komuna fizika modelo de botelo de Klein estas de simila konstruado. La Brita Scienca Muzeo estas elmontrata kolekto de manfaritaj vitraj boteloj de Klein, eksponantaj multajn variadojn pri ĉi tiu topologia temo.^[1]

Sekco |

Sekco de botelo de Klein rezultiĝas je filmoj de Möbius.

Sekco de botelo de Klein en duonoj laŭ ĝiaj simetriebenaj rezultiĝas en du spegulaj variantoj de filmo de Möbius. Eblas ankaŭ tranĉi la Botelo de Klein en solan filmon de Möbius.

Parametrigo |

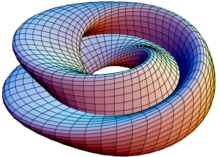
La figuro-8 mergo de botelo de Klein.

La figuro-8 mergo de botelo de Klein tranĉita.

La cifero-8-simila mergo de botelo de Klein havas aparte simplan parametrigon:

x=(r+cos⁡u2sin⁡v−sin⁡u2sin⁡2v)cos⁡u{displaystyle x=left(r+cos {frac {u}{2}}sin v-sin {frac {u}{2}}sin 2vright)cos u}

y=(r+cos⁡u2sin⁡v−sin⁡u2sin⁡2v)sin⁡u{displaystyle y=left(r+cos {frac {u}{2}}sin v-sin {frac {u}{2}}sin 2vright)sin u}

z=sin⁡u2sin⁡v+cos⁡u2sin⁡2v{displaystyle z=sin {frac {u}{2}}sin v+cos {frac {u}{2}}sin 2v}

En ĉi tiu mergo, la sinsekca cirklo estas geometria cirklo en la xy ebeno. La pozitiva konstanto r estas la radiuso de ĉi tiu cirklo. La parametro u donas la angulo en la xy ebeno, kaj v precizigas la pozicion ĉirkaŭ la "8" formita kruca sekcio.

La parametrigo de la 3-dimensia mergo de la botelo estas multe pli komplika. Jen estas simpligita versio:

x=2f(u)cos⁡ucos⁡v(3cos2⁡u−1)−2cos⁡2u80π3g(u)−3cos⁡u−34{displaystyle x={frac {{sqrt {2}}f(u)cos ucos v(3cos ^{2}u-1)-2cos 2u}{80pi ^{3}g(u)}}-{frac {3cos u-3}{4}}}

y=−f(u)sin⁡v60π3{displaystyle y=-{frac {f(u)sin v}{60pi ^{3}}}}

z=−2f(u)sin⁡ucos⁡v15π3g(u)+sin⁡ucos2⁡u+sin⁡u4−sin⁡ucos⁡u2{displaystyle z=-{frac {{sqrt {2}}f(u)sin u,cos v}{15pi ^{3}g(u)}}+{frac {sin ucos ^{2}u+sin u}{4}}-{frac {sin u,cos u}{2}}}

kie

f(u)=20u3−65πu2+50π2u−16π3{displaystyle f(u)=20u^{3}-65pi u^{2}+50pi ^{2}u-16pi ^{3}}

g(u)=8cos2⁡2u−cos⁡2u(24cos3⁡u−8cos⁡u+15)+6cos4⁡u(1−3sin2⁡u)+17{displaystyle g(u)={sqrt {8cos ^{2}2u-cos 2u(24cos ^{3}u-8cos u+15)+6cos ^{4}u(1-3sin ^{2}u)+17}}}

por 0 ≤ u < 2π kaj 0 ≤ v < 2π.

En ĉi tiu parametrigo, u sekvas la longon de la botela korpo kaj v iras ĉirkaŭ ĝia cirkonferenco.

Pli alta genro |

La artikolo fundamenta plurlatero provizas priskribon de la ĝeneraligoj de botelo de Klein de pli altaj genroj.

Vidu ankaŭ |

• Filmo de Möbius


• Reela projekcia ebeno


• Cilindro


• Sfero


• Toro


• Topologio


• Algebra topologio

Eksteraj ligiloj |

1. 
   ↑ Strangaj Surfacoj: Novaj Ideoj
   

• Eric W. Weisstein, Klein Botelo en MathWorld.


• 
  Botelo de Klein en PlanetMath.


• Pri la teorio de surfacoj de klein [1]
  


• Clifford Stoll fabrikas botelojn de Klein kaj vendas ilin je [2].


• La Klein Botelo


• La plej granda Botelo de Klein en la mondo


• 
  [3] Animacio
  


• 
  Botelo de Elkin montras 3D prezenton de botelo de Klein. La nomo "Elkin" estas anagramo de la vorto "Klein".