Kdjykuj

Regula oklatero
Simbolo de Schläfli	{8} t{4}
Figuro de Coxeter-Dynkin
Verticoj	8
Lateroj	8
Geometria simetria grupo	Duedra simetrio (D8)
Areo	2(1+2)t2{displaystyle 2(1+{sqrt {2}})t^{2}} ≃4.828427t2.{displaystyle simeq 4.828427t^{2}.} (t estas la latera longo)
Ena angulo	135°
v • d • r

En geometrio, oklatero estas plurlatero kun 8 lateroj.

Regulaj oklateroj |

Regula oklatero estas oklatero kiu estas regula plurlatero.

Ĉe konveksa regula oklatero ĉiuj lateroj estas egalaj kaj ĉiuj enaj anguloj estas 135°. Ĝia simbolo de Schläfli estas {8}.

Stelooklatero montrita per ruĝaj linioj

Nekonveksa regula oklatero estas 8-latera stelo, stelooklatero. Ĝia simbolo de Schläfli estas {8/3}.

Neregulaj oklateroj
Konveksa	Nekonveksa	Nekonveksa sinkrucanta (kompleksa)

Regula oklatero estas konstruebla kun cirkelo kaj liniilo. Unu el variantoj konstrui ĝin estas jena:

• Konstrui kvadraton.


• Konstrui ĉirkaŭskribitan cirklon ĉirkaŭ la kvadrato (eble ĝi jam estos konstruita dum la konstruo de la kvadrato).


• Disdividi ĉiun arkon de la ĉirkaŭskribita cirklo inter du najbaraj verticoj de la kvadrato je du egalaj duonoj.


• Verticoj de la kvadrato kune kun la mezpunktoj de la arkoj estas 8 verticoj de la regula oklatero.

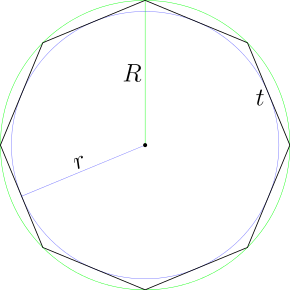
La areo de regula oklatero de flanka longo a estas

A=2cot⁡π8t2=2(1+2)t2≃4.828427t2{displaystyle A=2cot {frac {pi }{8}}t^{2}=2(1+{sqrt {2}})t^{2}simeq 4.828427t^{2}}

kie t estas la longo de latero

A=4sin⁡π4R2=22R2≃2.828427R2{displaystyle A=4sin {frac {pi }{4}}R^{2}=2{sqrt {2}}R^{2}simeq 2.828427R^{2}}

kie R estas radiuso de la ĉirkaŭskribita cirklo

A=8tan⁡π8r2=8(2−1)r2≃3.3137085r2{displaystyle A=8tan {frac {pi }{8}}r^{2}=8({sqrt {2}}-1)r^{2}simeq 3.3137085r^{2}}

kie r estas radiuso de la enskribita cirklo

A=S2−t2.{displaystyle A=S^{2}-t^{2}.}

kie S estas distanco inter la paralelaj lateroj, S=(1+2)t{displaystyle S=(1+{sqrt {2}})t}.

La lasta formulo estas pruvata per konsidero de kvadrato, kiu estas konstruita plilongigo de du paroj de paralelaj lateroj de la oklatero. Tiam inter la kvadrato kaj la oklatero aperas kvar 45-45-90 trianguloj. Se meti la triangulojn kune tiel ke la ortoj estas kune rezultiĝas la pli malgranda kvadrato, latero de kiu estas egala al latero de la oklatero. Areo de la unua kvadrato estas S², areo de la dua kvadrato estas t², areo de la fonta oklatero estas diferenco inter areoj de la kvadratoj.

Oklateroj en pluredroj kaj kahelaroj |

La senpintigita kvadrata kahelaro havas 2 oklaterajn edrojn ĉirkaŭ ĉiu vertico.	La senpintigita kubo havas 6 oklaterajn edrojn.	La senpintigita kubokedro havas 6 oklaterajn edrojn.
La oklatera prismo havas du oklaterajn edrojn.	La oklatera kontraŭprismo havas du oklaterajn edrojn.	La vertica figuro de la uniforma pluredro granda durombo-dudek-dekduedro estas enhavita en neregula stelooklatero, kun kvar lateroj tra ĝia centro.

Uzoj de oklateroj |

En multaj partoj de la mondo, halta signo havas formon de regula oklatero.	elektra butono de formo de regula oklatero	Ujo por salo de formo de regula oklatero
Skatolo de formo de neregula oklatero	Korbo de formo de neregula oklatero	Ombrelo de formo de regula oklatero

Vidu ankaŭ |

• Oklatera nombro

Eksteraj ligiloj |

• Eric W. Weisstein, Oklatero en MathWorld.


• Kiel trovi areon de oklatero


• 
  Difino kaj propraĵoj de oklatero kun interaga animacio